Dot Product of Two Vectors

It is a scalar quantity and is also called the dot product of vectors. We can also calculate the dot product between two vectors by using the dot function from the pracma library.

Dot Product A Plus Topper Reciprocalsystemofvectors Dots Commutative Positivity

Divide the dot product by the magnitude of the first vector.

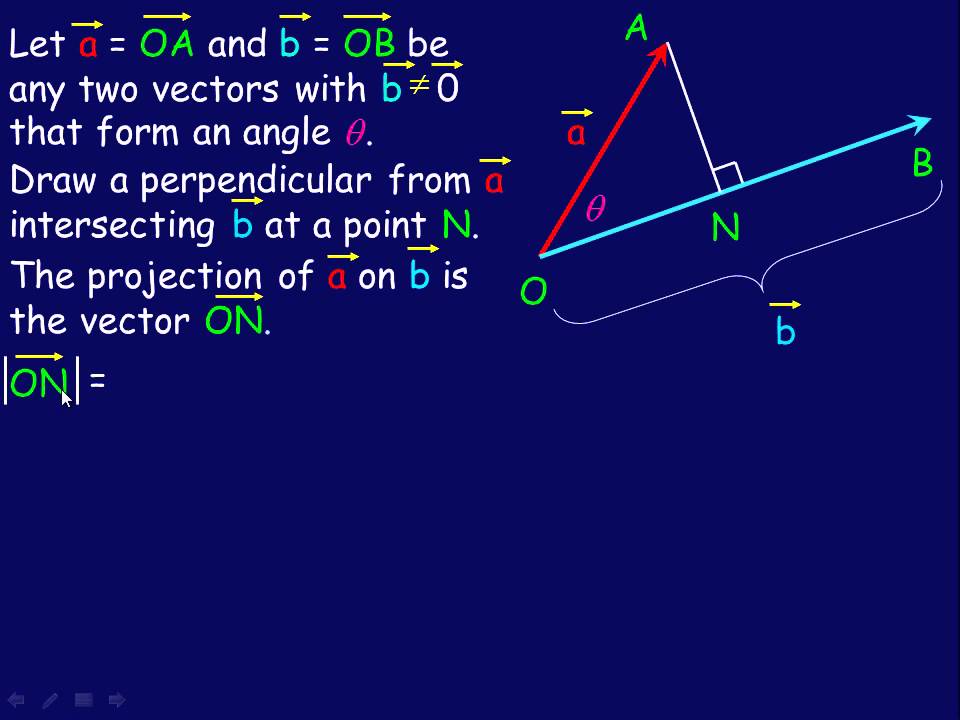
. The scalar product or dot product of two vectors is defined as follows in two dimensions. While this is the dictionary definition of what both operations mean theres one major. So by order of operations first find the cross product of v and w.

The main attribute that separates both operations by definition is that a dot product is the product of the magnitude of vectors and the cosine of the angles between them whereas a cross product is the product of magnitude of vectors and the sine of the angles between them. Result of dot product in the form of Matrix Product. Therefore the answer is correct.

A b This means the Dot Product of a and b. In other words the scalar product is equal to the product of the magnitudes of the two vectors and the cosine of the angle between them. Dot Product and Cross Product.

And would anyone agree that an inner product is a term used when discussing. It is often called the inner product or rarely projection product of Euclidean space even. Two vectors can be multiplied using the Cross Product also see Dot Product.

So if you multiply the matrix between them the. Find a b when a and b a b. Let θ be the angle between them.

Divide the resultant by the magnitude of the second vector. The dot product gives us a very nice method for determining if two vectors are perpendicular and it will give another method for determining when two vectors are parallel. This dot product is widely used in Mathematics and Physics.

In the general case the angle between two vectors is the included angle. The magnitude length of the cross product equals the area of a parallelogram with vectors a and b for sides. Let us find the angle between vectors using both and dot product and cross product and let us see what is ambiguity that a cross product can cause.

In mathematics the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers usually coordinate vectors and returns a single numberIn Euclidean geometry the dot product of the Cartesian coordinates of two vectors is widely used. They can be multiplied using the Dot Product also see Cross Product. For vectors a a 1 a 2 a 3 and b b 1 b 2 b 3the dot product can be found by using the following formula.

A is the magnitude length of vector a. In 3D and higher dimensions the sign of the angle cannot be defined because it would depend on the direction of view. Let us compute the dot product and magnitudes of both vectors.

Note as well that often we will use the term orthogonal in place of perpendicular. α arccosx a x b y a y b x a 2 y a 2 x. Skip to navigation Press Enter Skip to main content Press Enter Home.

I was wondering if a dot product is technically a term used when discussing the product of 2 vectors is equal to 0. Once again the dot product between the two vectors turns out to be 35. Then dot that with u.

So if we take two vectors one has to be written in the form of row matrix and the other in the form of column matrix. Math 2241 Spring 2022. You need a third vector to define the direction of view to get the information about the sign.

We can calculate the dot product for any number of vectors however all vectors must contain an equal number of terms. The cross product is mostly used to determine the vector which is perpendicular to the plane surface spanned by two vectors. The full version.

0. The Cross Product a b of two vectors is another vector that is at right angles to both. Note that the operation should always be indicated with a dot to differentiate from the vector product which uses a times symbol --hence the names dot product and cross product.

A b a 1 b 1 a 2 b 2 a 3 b 3. Ab ab cos θ. The Vector product of two vectors is of two types.

Given vectors u v and w the scalar triple product is uvXw. Use the dot function. Dot product is also known as scalar product and cross product also known as vector product.

Dot Product Let we have given two vector A a1 i a2 j a3 k and B b1 i b2 j b3 k. Mathematically angle α between two vectors can be written as. Library pracma define vectors a.

A b 1-2 -21 -2. This physics and precalculus video tutorial explains how to find the dot product of two vectors and how to find the angle between vectors. And it all happens in 3 dimensions.

We can calculate the Dot Product of two vectors this way. You will notice many science books or research papers where dot products are written as the product of row and column matrix. Find the dot product of two or more vectors with an equal number of terms.

In mathematics an inner product space or rarely a Hausdorff pre-Hilbert space is a real vector space or a complex vector space with an operation called an inner product. The dot product of two different vectors that are non-zero is denoted by ab and is given by. As always this definition can be easily extended to three dimensions-simply follow the pattern.

The inner product of two vectors in the space is a scalar often denoted with angle brackets such as in Inner products allow formal definitions of intuitive geometric notions such as lengths angles. The scalar product of two vectors is equal to the product of their magnitudes. A b a b cosθ Where.

Where i j and k are the unit vector along the x y and z. How to multiply matrices with vectors and other matrices. Evaluate the determinant youll get a 3 dimensional vector.

Find the dot product of the vectors. Set up a 3X3 determinant with the unit coordinate vectors i j k in the first row v in the second row and w in the third row. Stack Exchange network consists of 182 QA communities including Stack Overflow the largest most trusted online community for.

Multiplying matrices and vectors. Here are two vectors. In this article we would be discussing the dot product of vectors dot product definition dot product formula and dot product example in detail.

The dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number. The Dot Product is written using a central dot. A vector has magnitude how long it is and direction.

There are two vector A and B and we have to find the dot product and cross product of two vector array. The scalar product of two vectors is the sum of the product of the corresponding components of the vectors. Now if two vectors are orthogonal then we know that the angle between them is 90 degrees.

Angle Between Two Vectors in 2D Using Dot Product. Therefore two perpendicular vectors will have a dot product of zero. To calculate the angle between two vectors in a 2D space.

Applications Of The Dot Product Avi Calculus Mathematics 12th Maths

Dot Product A Plus Topper Reciprocalsystemofvectors Dots Positivity Commutative

Dot Product Explained Vector Calculus Calculus Mathematics Geometry

Product Of Vectors Vector Multiplication Vector Can

How To Find The Scalar And Vector Product Of Two Vectors Easily How To Find Dot And Cross Product

How To Memorize Things Commutative Vector